2019 年电子科技大学 ACM-ICPC 暑假前集训图论专题解题报告

Posted on 2019-06-09 In OI/ICPC

10/15/15

A. 迷宫

题目描述

给出一个有向图，反转一条有向边的代价为其边权，现在选出一些边进行边反向操作，代价为选出边权值的最大值，求一个最小代价使得有向图无环。

数据范围：。

题解

求一个最大值最小的问题一般考虑二分答案，判断有向图无环问题一般用拓扑排序解决。两者拼一下就过了……

首先考虑到答案的可二分性质。考虑检查答案时，只保留边权大于要检查的答案的所有边，小于等于答案的所有边舍弃不加。如果这些边已经出现环的话，答案一定向大的方向调整，如果不存在环，那么考虑将剩余的边补回去，就按照已有的拓扑序补充即可，并且按照已有拓扑序，加入边要么正常加入，要么反向以满足拓扑序。所以答案一定是可以满足的，可以继续调整减小答案。

原题题解中给出的一种的做法其实是对边权进行离散化……

时间复杂度，空间复杂度。

原题详见：Codeforces Round #532 (Div. 2) E. Andrew and Taxi

代码见这里

B. oydy 的征途 I

题目描述

给出一个无向图，求其最小生成树边权和减去最大边的值，和有多少种选择第一条边的方案能使生成树边权和减去最大边权值等于第一问的答案。

数据范围：。

题解

对于第一问，显然直接做一遍最小生成树即可。

对于第二问，如果我们保持原最小生成树小于最大边权的边不变，那么再加入大于等于这个最大边权的边答案一定是不变的（有多条最大边权的边时，存在方案补充边并保持答案不变），但是要保证树的性质，所以不能出现环。因此我们把原最小生成树中小于最大边权的边连起来，判断一下剩下的边是否连通即可。如果不连通，则说明这条边可以加入，并且边权和不变。

时间复杂度，空间复杂度。

代码见这里

C. oydy 的征途 II

题目描述

给出一个有向图，求经过每条边恰好一次，经过点序列中字典序最小的一个。

数据范围：。

题解

欧拉路径板子题。有向图中存在欧拉路径的充分条件是：基图连通（把边当成无向边，不考虑度为的点），每个顶点出度等于入度或者有且仅有一个点的出度比入度多，有且仅有一个点的出度比入度少，其余出度等于入度。

如果存在欧拉路径的话，点序列长度一定是，那么就按照字典序遍历节点即可。

先是存答案不按板子里存 WA on 8，然后判断是否连通 WA on 15，然后改掉 TLE on 28，最后加了一个丑陋的删边 RE on 29（拿队列删边真的我服了我自己……），能踩的坑都踩了一遍，最后心态炸了手写栈，过了。

时间复杂度，空间复杂度。

代码见这里

D. oydy 的征途 III

题目描述

一个无向图，问按顺序经过给定个点的最短路。

数据范围：。

题解

因为要求最短路程，所以走的距离一定是给出的要经过的相邻点之间的最短路。于是题目变成了次询问两点之间最短路长度，最后输出的就是最短路长度之和。

当时很容易处理，就是多次询问树上点之间的距离。

当时，即多了一条边的情况，那么这条边就有两种情况：对最短路有贡献和对最短路没贡献。如果对最短路没贡献，那么还是询问树上两点距离；如果有贡献，那么直接求这条边的两端点之一到询问两点的最短路长度之和就行了。

对于边数更多的情况，实质上和的情况一样。我们记一下「多出来」的边的一个端点，即加上这些「多出来」的边，树就会出现环。因为最短路改变只能由这些「多出来」的边引起，如果不变的话就是树上距离，因此正确性可以保证。

对于树上询问两点间路径，可以用 LCA 解决。对于寻找这些「多出来」的边的一个端点，在 LCA 的准备阶段就可以解决。然后对于这些点跑单源最短路，用这些最短路更新答案即可。

时间复杂度，空间复杂度。

原题详见：Educational Codeforces Round 51 (Rated for Div. 2) F. The Shortest Statement

代码见这里

E. 变色龙

题目描述

给定一个无向图，每条边都有颜色，通过一条边的条件是目前颜色和要通过边的颜色一致，代价不计。变换颜色花费为，并且只能在一个点处变换颜色，求从走到的最小花费。

数据范围：。

题解

看起来很像拆点建边，思路是一个点拆成三个点，其中一个点为入点，两个为出点，分别表示在这个点变换颜色还是不变颜色，然后一个水最短路就行了。但是建图不知道为啥爆炸了……

于是对于点的每种状态重建图，对点的每个颜色状态建立一个点，原图中相连接的两点在新图中变成两端点分别向这条边对应的颜色状态建边权为的边，表示转换颜色，然后两点相同颜色状态之间连边权为的边，表示走这条路的代价。

如果要转换颜色，则走边权为的边就表示转换颜色了，否则可以走新点建立的边权为的边越过边权为的边。

例如原图如下：

边上的数字表示边的颜色。

那么我们重建的图如下：

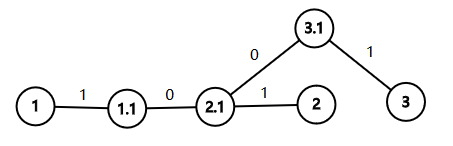
边上的数字表示边权。

这样建图，点数最多为，边数最多为，还不算特别爆炸。

注意最后答案需要除以，因为按照这样的拆点方法，原来距离为的两点距离变成了（可以从到的路径中看出），原来距离为的两点距离仍为，因此求完最短路是答案的二倍。

时间复杂度，空间复杂度。

原题来自：HNCPC2016 地铁

代码见这里

F. zh 吃饭

题目描述

给出一个有向图，每个点都有点权，给出一个起点和一些终点，每次到达一个点能获得这个点的点权，但是这个点的点权在获得后变成，求从起点到终点可能获得的最大权值。

数据范围：。

题解

对于这个有向图，首先权是点权，其次只能获得一次点权，那么可以将这张图进行缩点，把强连通的点缩成一个，然后对于缩出来的 DAG 做一遍最长路 DP 即可。注意原图起点和终点缩进了强连通分量中，注意标号问题。最后取一个最大值即可。

强连通分量的点一定可以互相可达，因此可以获得这些点的所有权值，统计出每个缩出来的点的权值后进行 DP，记忆化搜索爆栈了所以改成了 BFS……

时间复杂度，空间复杂度。

代码见这里

G. hqf 吹泡泡

题目描述

给出个点和条边，并且给出一些可以连接的点连接起来的代价，求一个最小代价加边使得这个点形成个连通块。

数据范围：。

题解

看起来是最小生成树，实际上加一行就行了……

因为要求个连通块，所以加入条边即可。形成棵树就是个连通块。

剩下的与最小生成树无异。

时间复杂度，空间复杂度。

原题详见：Luogu P1195 口袋的天空

代码见这里

H. 毁灭东湖计划

题目描述

~~给出一些点和一些边，每条边有流量，求起点到终点的最大流量。~~

求最大流。

题解

Dinic 板子，用之前写的 EK 过不了可能是因为写错了……

时间复杂度，空间复杂度。

原题来自：POJ 1273 Drainage Ditches

代码见这里

I. cxx 仙女下凡

题目描述

给一个个点条边的有向图，求短路。每一条路都不能完全相同。

数据范围：。

题解

最后那个条件让我 WA 好几遍……

短路也是板子……结果板子调用错了……WA 到头秃……

考虑利用 A* 算法搜出短路，存一遍反图，跑反图的最短路并用其估价，这样跑遍出来就是短路了。

注意起点与终点相同时需要变成，因为首先搜出来的一定是一个，就是没动，但是这种情况不能计入答案。

时间复杂度，空间复杂度。其中用来描述 A* 的复杂度（实际上并没有啥意义……）。

代码见这里

J. cxx 守株待兔

题目描述

~~啊不想概括了~~

求二分图最小点覆盖。

数据范围：。

题解

二分图最小点覆盖等于二分图最大匹配数。所以用 Dinic 做一遍二分图最大匹配即可。

用 Dinic 做二分图最大匹配时间复杂度很好~~，时间复杂度是一个大的取最小值式子但是我忘了……~~

时间复杂度，空间复杂度。

~~算了时间复杂度写吧……~~

代码见这里

K. cxx 承包鱼塘

题目描述

给出一个个点条边的无向图，边有边权，可以有次机会令边权为，求的最短路。

数据范围：。

题解

的情况就是最短路，那么就可以有一个 DP。表示到第个点，用了次边权置为的最短路，转移什么的过于显然不写了。总体就是决策用和不用置的情况，取一个最小值即可。

其实是一个比较板子的分层图，那个 DP 的转移直接写进最短路即可……

时间复杂度，空间复杂度。

原题来自：「JLOI 2011」飞行路线

代码见这里

L. cxx 的压岁钱

题目描述

有个人个电视频道，每个人有一些想要看的电视频道，如果这个人看到了所有想看的电视频道就会给一些钱，开通一个电视频道要花一些钱，求最大利润。

数据范围：。

题解

~~把网络流 24 题都做了一遍也看不出来这个是太空飞行计划应该洗洗睡了……~~

我们把电视频道和人都看成一个点，那么点有点权（电视频道的点权为负），人向想看的电视频道建边，最后补充超级源汇，可以转化为最大权闭合子图问题。刨坟把原来写的题解挖出来完事。

于是一遍最小割就完事了……

但是我边空间开小了倍还是过了不知道咋回事……

时间复杂度，空间复杂度。

原题详见：LibreOJ #6001. 太空飞行计划

代码见这里

M. 洁姐姐带找工作

题目描述

有三种大小关系：，给出个变量间的组关系，求是否有方案可以满足全部关系，如果有，求最小的。

题解

转化为差分约束问题，对于就变成，对于变成，对于就变成。然后套差分约束板子即可。

对于有无解判断，直接判断是否有负环即可，对于最小解的判断，可以加一个基准，可以发现，还是符合差分约束条件的，一起差分约束即可。

时间复杂度，空间复杂度。

原题来自：SCOI 2011 糖果

（实际上是弱化）

代码见这里

N. 洁姐姐带我上分

题目描述

狼羊过河，只不过狼羊关系不止一种。

数据范围：。

题解

考虑数据范围，可以利用状压解决。用二进制状态表示目前在低段位的人，那么初始状态就是，终了状态就是。

首先筛选出合法状态，就是有狼羊关系的两人不能在第一个人不在的情况下同时处于低段位或高段位，这里注意要判两次，低段位判一次，此时的高段位情况就是，再对这个状态判断一次。

然后就会筛出一些合法状态。然后合法状态相互连边，如果两个合法状态中，人状态改变量大于则不能连边，因为要让第一个人带着去，所以第一个人的状态一定改变，不变的不能连边，最后还有如果要从低段位带到高段位，现有状态在高段位的人不能变成下一个状态在低段位，同理，从高段位带到低段位也是不能出现低段位有人跑到高段位上来。判断这个有一个巧妙的方法：令两个状态为，状态改变的情况可以用异或求出，即，那么，则这两个状态可以互相转移。这个是利用二进制的操作进行的。边权为的二进制中的个数。

于是跑一遍最短路就行了。数据没有很多或者很小的情况，因此跑不满……

时间复杂度，空间复杂度。

代码见这里

O. 洁姐姐带学画画

题目描述

对于平面上的个点，求一棵生成树，使得最小，其中表示两点的水平距离。

数据范围：。

题解

看到那个比值式求最小……其实想到的是 01 分数规划……

01 分数规划是用二分做的，所以相应的我们采用同样的方式，二分答案来做。

对于二分到的答案，我们要令。这个分式看起来很不爽，于是将分母乘过去，得：

移项，得：

（如果移项移反了就能求最大值了……）

对于检查这一答案是否合法的过程，令，如果对于这一边权建立最小生成树，权值和仍大于，那么这个必定不合法，需要增大以使权值减小，否则可以减小来减小答案。二分至精度要求即可。

对于求一个完全图的最小生成树，利用 Prim 算法比 Kruskal 要更优秀，毕竟少个嘛……

时间复杂度，空间复杂度。

原题来自：POJ 2728 Desert King

代码见这里