2019 年电子科技大学 ACM-ICPC 暑假前集训字符串与搜索专题解题报告

Posted on In

11/19/19

注意：以下若无特殊说明，将目标串 的长度 或目标串长总和 简记为 ，将模式串 的长度 或模式串长总和 简记为 。这样简记是由于一般字符串数量对于时间复杂度没有影响，主要是字符串长度或总长度影响时间复杂度。如果字符串数量对时间有影响的话将用回原用符号。

A. qh 与复读机 I

题目描述

维护一个字符串数组，支持在结尾插入一个字符串，查询最后一个字符串是前面多少个字符串的前缀和后缀。

数据范围：。

题解

对于统计一个字符串是一个字符串集合中多少个字符串的前缀，有一个经典的 Trie 树做法，将字符串插入 Trie 树中并统计一个节点经过的次数。查询时输出这个被查询字符串最后一个字符对应节点的出现次数即可。

对于后缀，把字符串倒过来就与统计前缀的情况一样了……

根据题意，需要先查询后插入。

时间复杂度：，空间复杂度：。

代码见这里

B. qh 与复读机 II

题目描述

给一个字符串，问字符串的周期。

数据范围：。

题解

上去读错题，于是挂了五发哈希。

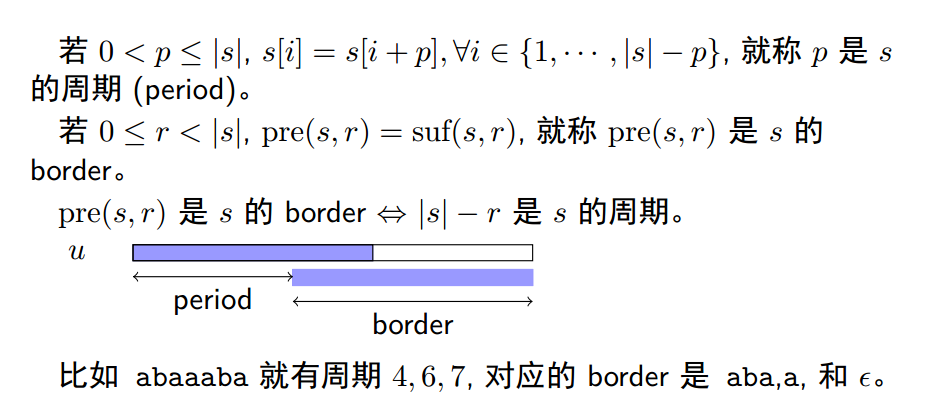
（来自 WC 2017 字符串算法选讲 By 金策）

嘿嘿，嘿嘿嘿，嘿嘿嘿嘿嘿。

于是迭代 nxt 数组即可。

时间复杂度 ，空间复杂度 。

如果用哈希的话需要注意字符集大小和字符对应的数字值，即注意 a 和 aa 两个串。

代码见这里

C. qh 与复读机 III

题目描述

给出目标串 和模式串 ，求出 在 中的所有出现位置。

数据范围：。

题解

裸 KMP 匹配，如果不明白的话重学数据结构与算法这门课。

时间复杂度 ，空间复杂度 。

代码见这里

D / E. qh 与复读机 IV / V

题目描述

（两道题一样，放一起写了）

给定目标串 ， 次询问每一个模式串 出现次数。

数据范围：。

题解

先写了个 KMP， 的居然过了 40 个点……

对于统计出现次数的问题，可以利用 AC 自动机求解。其实就是把文本串放到 AC 自动机上进行匹配，沿着 fail 指针爬上去，给有以这个节点结束的字符串答案加一。

这样统计答案复杂度就炸了过不了最后一个点，于是考虑将答案合并统计，每次只给这个节点的出现次数加一，最后统计每个字符串结束节点的出现次数即可。

时间复杂度 ，空间复杂度 。

D 题代码见这里
E 题代码见这里

F. qh 与复读机 VI

题目描述

给定两个字符串 ，求三元组 的数目并满足：

  • ；
  • ；
  • ；
  • 串中第 个到第 个字符组成的字符串与 串中第一个到第 个字符组成的字符串连起来是个回文串。

数据范围：。

题解

对于合法的三元组，都有 反转后与 相同。因为从 串中截取的子串长度要大于 串截取的前缀长度，因此我们可以将 串分成两部分， 串的前一部分反转后与 的一个前缀相同，后半部分是一个回文串。对于总体的统计，就相当于对于每个 ，求 与 的最长前缀长度与以 为结尾的回文串个数之积，答案为它们的和。

对于求以每个位置为结尾的回文串个数，可以通过回文半径进行差分求出。

对于求一个串后缀与另一个串前缀的最长前缀长度，这个用扩展 KMP 即可。

原题来自：2018-2019 ACM-ICPC, Asia Nanjing Regional Contest M. Mediocre String Problem。

时间复杂度 ，空间复杂度 。

代码见这里

G. qh 与复读机 VII

题目描述

求本质不同的数字回文串之和。对 取模。

数据范围：。

题解

回文自动机板题，对给定的串创建回文自动机，最后在自动机上深搜统计一下即可。

时间复杂度 ，空间复杂度 。

代码见这里

H. qh 与复读机 VIII

题目描述

给出一些字符串，每个字符串对应一个权值。现利用这些字符串构造一个长为 的字符串，每个字符串对长为 的字符串的贡献为出现次数与权值的乘积，求最大贡献。

数据范围：。

题解

首先看 I 题的题解。

这道题和 I 题其实是类似的，只不过求的是权值与出现次数的乘积之和还得求最大值。改一下 I 题的矩阵，Trie 树中每个字符串结束节点加上该字符串权值，沿 fail 树统计时继承子节点的权值，然后在 Trie 树上统计父节点转移到子节点的权值。矩阵乘法改成类似 Floyd 的转移，其实类似求个最长路。然后接着沿用矩阵快速幂。统计一下答案就完事了。

原题来自：Codeforces Round #362 (Div. 1) D. Legen...

时间复杂度 ，空间复杂度 。

代码见这里

I. qh 与复读机 IX

题目描述

一共有 个禁止出现的单词，保证单词中只出现小写字母，求构造一个不长于 的小写字符串，使得这一字符串出现至少一个禁止的单词的方案数。

数据范围：。

题解

下面考虑仅对构造长为 的字符串的情况。

考虑转化问题为求任何禁止的单词都不出现的方案数，那么答案就是 减去这个方案数。

考虑 AC 自动机的匹配过程，在 AC 自动机上匹配的时候，由 fail 树经过 次转移到达某个结点，这个结点所代表的字符串可以看作长度为 的字符串的后缀，顺着字典树往下跑可以转移到新的长 字符串。所以统计一下树上从一个节点到另一个节点有多少种合法转移情况，就转化成了以下问题：已知图上两个节点转移有 种方式，求起点到终点长为 的不同路有多少种，这个其实就求矩阵 就行了。对于合法的转移，我们将每个单词插入 Trie 树中，然后标记一下结束节点。如果一个节点沿 fail 树转移到了结束节点，那么为避免出现禁止的单词，这个节点也应该继承结束标记。

考虑求全部答案的情况，我们其实要求的是一个前缀和，那么构造矩阵的时候多加一个全为 的列向量，就可以实现求前缀和了。求矩阵的幂利用矩阵快速幂可以求解。求总方案数是一个等比序列求和，求一下逆元即可得出全部答案，最后减去不出现禁止单词的答案数就是最终答案了。

原题来自：HDU 2243 考研路茫茫

时间复杂度 ，空间复杂度 。

代码见这里

J. qh 与复读机 X

题目描述

给出一些单词，问每个单词在全部单词中出现了多少次。

数据范围：。

题解

考虑还是 AC 自动机，这个和 DE 题是一样的，先把单词插入 AC 自动机，再把单词连起来和 DE 一样做就完事，但是每两个单词之间插入一个 # 分隔开就行了。

有没有一些优雅的解法呢？有的，还是考虑 DE 两题，加答案的时候其实就是沿 fail 树往上爬，每次答案加上以这个点为终点的字符串个数，这次变成全部的情况，所以最后 BFS 一遍 fail 树，一个字符串结束节点的子树大小就是这个字符串的出现次数了。

原题来自：TJOI 2013 单词

时间复杂度 ，空间复杂度 。

代码见这里

K. qh 与复读机 XI

题目描述

给一个字符串，问长度为 的子串中出现次数最多的子串的出现次数是多少。

数据范围：。

题解

写题解之前先吐槽一下……明明原版论文写的就是 为啥用 ……

考虑直接用后缀自动机，考虑 集合，即表示一个子串结束位置的集合。我们计算 SAM 中所有节点的 集合大小，就求出了所有串的出现次数。根据性质，Parent 树的节点父节点的 集合真包含这个节点的 集合，所以考虑从 Parent 树自底向上更新父节点的 集合，然后更新串长为一个值的答案即可。

原题来自：SPOJ Substring

时间复杂度 ，空间复杂度 。

代码见这里

L. qh 与复读机 XII

题目描述

给出一个字符串，多次询问 在 中出现的次数。

数据范围：。

题解

考虑看到这道题就想到一些鬼畜 NOI 模拟题，就不想做了。

阿狸的打字机一题是 的情况，所以我们可以按照阿狸的打字机那么做，那道题离线，这道题也离线。就按阿狸的打字机做，然后答案减去 和 的出现次数就完事。

好了，我们拆三遍做，第一遍做 的，剩下两遍做后面两个，好，我们搞出来了一个没啥用的方法，因为需要动态 AC 自动机，就变成 NFA 了……CDQ 做不了，莫队做不了，NFA 也不会转化成 DFA，SAM 能不能做也不知道，但是问题转化成了询问字符串的一个子串在字符串前缀中的出现次数。

考虑 SAM 的 parent 树的性质，就是以一个节点为根的子树上所有节点都以这个节点代表的字符串集合为后缀。所以以这个点为根的子树就是这个点代表的字符串的所有出现位置。

先用倍增法找到目标串，目标串可以看做原串前缀的后缀，所以先找到 的位置，这个可以在 SAM 的插入过程中记录，然后往上爬这个串的长度层即可，这个可以用倍增法解决。

然后考虑对于一个前缀的询问，我们只需要将这个前缀的所有前缀代表节点权值加一，然后统计目标串对应节点的子树权值和就是答案了。

于是对于并非前缀的询问，就可以拆成两个前缀做，然后得到的结果作差就是答案了。这里用到了可持久化线段树。将每个前缀作为一个版本，然后查询就是两个版本区间和的差。区间就是目标串的子树区间。

时间复杂度 ，空间复杂度 。

代码见这里

M. 一切的开始，世界树的测验

题目描述

一共有 个数，最多改变 个数，使得 变为 ，求有多少种方案可以从这个数组中选出一些数，它们的和为 。

数据范围：。

题解

每个数有三种决策：不变也不加到答案中，不变但加到答案中，变且加到答案中（变但不加到答案中没有用，因此不统计）。所以显然有一个 的暴力。

考虑 Meet in the middle，就行了……

时间复杂度：，空间复杂度 。

代码见这里

N. 第一个征程，噩梦的开始

题目描述

给一个地图，从起点出发，最多向左走 格，向右走 格。求能够到达的格子个数。

数据范围：。

题解

首先注意到直接 BFS 是错误的，因为样例根本过不去。

考虑从 走到 这一过程，我们向左走了 步，向右走了 步，那么 ，移项得 。由于 在一个网格中是确定的，所以只要最小化 ，就相当于最小化 ，所以我们优先走上下方向，然后再扩展左右即可达到最优状态。利用双端队列进行 01 BFS 即可。

原题来自：Codeforces Round #516 (Div. 1, by Moscow Team Olympiad) B. Labyrinth

时间复杂度 ，空间复杂度 。

代码见这里

O. 第二个征程，拔起剪枝哀伤

题目描述

有一个数列 ，构造一个数列 ，使得 ，要求 项数尽量小，输出按递增方式输出。

数据范围：。

题解

首先我们不知道 数列的长度，那么这就很尴尬，所以我们先枚举这个长度，也就是用加深迭代搜索。

然后搜索 数列每一位应该放什么，因为最后 数列是单调增的，所以我们从前往后搜索的时候就可以不管绝对值，然后 时，，就可以枚举 然后得到 了，注意得到 后还需进一步更新能表示的 。能表示的 这一集合可以用状态压缩的方法存储。

原题来自：UVa 1377. Ruler

代码见这里

P. 征程的结束，吉安娜

题目描述

给出一个华容道局面，多次询问给定活格，起点和终点的情况下起点到终点的最少步数。

数据范围：。

题解

考虑将起点移动到终点的过程，起点周围没活格一定动不了，所以先要把活格移到起点周围，然后才能把起点移动到终点。

所以分成两段考虑，把活格移动到起点的上下左右方向，然后把起点移动到终点。这样每次都要同时动两个格子，所以复杂度 过不去。

考虑活格和它相邻的格子，一条有效路径（即能够到终点的路径）上所有点的状态也就是 ，因为活格可以位于一个格子的上下左右四个位置。把这些状态记录下后，将这些状态之间的转化建有向边，起点到终点的最短距离就是一个最短路问题了。

这样，我们先 BFS 一遍，将活格移动到起点周围，然后再做一遍最短路，两条路长度相加即为答案。

因为第一遍移动的是活格不是棋子，如果要都用最短路的话需要一共五遍最短路，所以只用 BFS 一遍就可以了，常数很小。

原题来自：NOIP 2013 Day2 T3 华容道

时间复杂度 ，空间复杂度 。

代码见这里

Q. 猛男 24 点

若纳水輨，如转丸珠。夫岂可道，假体如愚。荒荒坤轴，悠悠天枢。
载要其端，载同其符。超超神明，返返冥无。来往千载，是之谓乎。

——《二十四诗品 · 二十四 · 流动》

题目描述

牌区初始有四张牌。有两个人 van ♂ you see，他♂们初始都有一些手牌，对于每次换牌，第一个人把自己的一张手牌放入牌区，然后扔掉牌区中的任意一张牌，第二个人会把自己的一张黑色手牌与牌区中的一张牌相交换。第一个人先手，每个人都可以在自己的轮内不换牌，除第一轮外，如果一个人不动，他就输了。如果牌区里的牌能凑出 24 点，则先手胜，否则后手胜。多次给出初始局面，问先手胜还是后手胜。

数据范围：，牌上点数是 到 之间的正整数，其中 分别为两人的手牌数。

题解

首先得打一个 24 点的表。嘿嘿，嘿嘿嘿。

反正是个 Dirty work，首先跑个暴搜，枚举 的所有长度为 的可重排列，再枚举运算符号，再处理一下运算优先级，复杂度算起来好像可以，但是最后还是直接打表。

注意除不尽的情况，用 double 或者用个逆元处理一下。最后只有 个方案。先打出来表，然后每一位减去 后用 进制压位，表大小 2KB 多一点，能交上去。

然后对于判断牌区局面，因为压位后数字大小都小于 ，所以开个 大小的 bool 数组，把所有状态存进去就行了，这下判局面就是 了。

然后就是搜两人的操作了。第一个人的目标是让牌区尽量是 24 点，而第二个人的目标是让牌区尽量不是 24 点。然后就根据这个进行操作即可。先判牌区是不是 24 点，对于第一个人还需要判断是不是第一次操作，因为第一次不操作不会导致游戏结束。如果是或不是 24 点，则返回对应输赢状态，否则进行搜索，用自己的哪一张牌换牌区中的哪一张牌，然后注意回溯和换的条件即可。

Dirty work 挺多……

代码见这里

R. 如果早知道 wf 题也会被 ak

题目描述

求一个字符串中最长偶回文字符串长度。其中偶回文字符串指长度为偶数的回文字符串。

数据范围：。

题解

考虑 Manacher 算法，对于构造的字符串，如果回文串长度为偶数，那么它的回文中心为添加的字符 #，所以检查所有字符为 # 的位置的回文串长度即可。

时间复杂度 ，空间复杂度 。

代码见这里

S. 如果早知道 wf 题也会被 ak - DLC1

题目描述

求两个字符串的 LCS 长度。

数据范围：。

题解

对于这个问题，有一个经典的 SA 解法。两个字符串之间加一个未出现的字符，并连接在一起，求出新字符串的 SA 和 height 数组。如果 SA 中相邻两个元素一个大于第一个串长，另一个小于第一个串长，则说明两后缀串有公共前缀，并且长度为后一个位置的 height 值。用它更新答案即可。

注意用 DC3 的时候空间开三倍，并且字符串长度是两个字符串长度之和，因此数组至少要开 的。

时间复杂度 ，空间复杂度 。

代码见这里