高级算法设计与分析课后内容个人解析

Posted on In

文章包含哈尔滨工业大学高级算法设计与分析课程作业、实验和大作业的个人解析。

四个实验可以参考这里。大作业可以选分布式一致性 hash，问题不大，资料也比较多（毕竟上课和面试八股里都有），可以参考 Stanford CS 168 的 Lecture 1，讲义很清楚，里面有一致性 hash 的出处论文。PPT 自己做吧，还得录音，哈哈。

原来以为这个研究会发 SOSP 或者 SIGCOMM 这种，但是居然发的是理论的 STOC。

最 nb 的是作业要手写，哈哈，给助教磕一个吧。为了整这堆东西，Skyplane 论文看得磕磕巴巴，DuVisor 的博客来不及写，网络算法学也好几周没看，认真整这玩意真的就输了。

第一次作业

一、证明：

设 ，。

令 ，当 时 所以 。

由于 其中对第一个不等号， 到 的乘积一定不小于舍去前 项的乘积。对于第二个不等号，将左边的每一个数均替换为 ，结果一定不变大，左边式中共有 项，因此同时将指数变小，结果一定不会变大。

所以 令 ，当 时 所以 。

从而 。

二、用迭代法解递归方程： 令 ，则 。

则有 所以 。

三、求解递归式： 令 ，则 ，假设 为常数，则有 所以 。

四、求解递归式：

根据 Akra–Bazzi 定理 该递推式满足定理适用条件，则 其中 ，即 。

即 ，也可以称 。

五、求解递归式：， 对 成立

根据 Master 定理，。取 ，则 。所以满足第一条使用条件，。

六、根据表达式 和 设计分治（或递归）算法求解下列问题，并分析算法的时间复杂度。

a. 输入实数 和自然数 ，输出实数 ；
b. 输入实数矩阵 和自然数 ，输出实数矩阵 。

a. 递归伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
Pow(a, n)
    if n = 0 then
        return 1
    if n = 1 then
        return a
    result := Pow(a, n / 2)
    if n mod 2 = 0 then
        return result * result
    else
        return a * result * result
    endif

可以写出递归式 ，使用迭代求解可知此算法时间复杂度为 。

b. 递归伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
PowMatrix(A, n)
    if n = 0 then
        return I
    if n = 1 then
        return A
    result := PowMatrix(A, n / 2)
    if n mod 2 = 0 then
        return result * result
    else
        return A * result * result
    endif

可以写出递归式 ，其中 为矩阵的规模。同样使用迭代求解可知时间复杂度为 。

七、给定平面上 个点构成的集合 。如果存在边平行于坐标轴的矩形仅包含 中的两个点 和 ，则称 和 为「友谊点对」。试设计一个分治算法统计 中友谊点对的个数。

首先考虑对于一个「友谊点对」，一定存在一个以这个点对为对角线的矩形包含这个点对。对于这个缩小的矩形退化为一条线段的情况，那么我们可以给长（或宽）加上一个无穷小量保证其为一个矩形而满足题目要求。因此问题可以规约到统计满足下列条件的点对数量：

  • 以这个点对为对角线的矩形内部或边界上（或退化成的线段上）没有其他点。

首先将所有点按 坐标排序。之后针对 坐标分治。分割过程如下：

  1. 计算这些点中 坐标的中位数 ；
  2. 用水平线 将点划分为两个集合。称为上半部分和下半部分；
  3. 计算点对中两点分别在上半部分和下半部分的时候对答案的贡献；
  4. 递归地计算上半部分和下半部分分别对答案的贡献。

对于边界情况，如果目前的点集为空集或只有一个点，则直接返回，如果只有两个点，则对答案有贡献 。

对于计算贡献部分，由于点对中两点分别位于上半部分和下半部分，所以仅需考虑上半部分的点作为左上或右上，下半部分的点作为左下或右下的情况。

考虑上下两部分 坐标均为递增顺序，如果选定上半部分的某一个点为右上角，那么下半部分所有 坐标小于等于上半部分选定点的就在考虑范围中。考虑按照 坐标递增的顺序枚举上半部分的每一个点，如果有 坐标相同的情况，则只考虑 坐标最小的那个，因为所有 坐标比它大的点构成的矩形一定包含 坐标最小的这个。令目前枚举到的上半部分点为 ，如果前一个点 的 坐标比 小，那么我们需要考虑的下半部分点的 坐标就要比 的 坐标大，否则如果下半部分考虑的 范围不比 的 坐标大，则会存在矩形包含 的情况，这样是不合法的；如果前一个点 的 坐标比 大，那么这些 坐标大的点不会进入以 为右上角的矩形，下半部分考虑的 范围就可以向左扩大到上半部分第一个 坐标比 小的点的 坐标，所有比这个 坐标大的点均在考虑范围中；如果前一个点 的 坐标等于 的 坐标，那么同样下半部分的 坐标只考虑大于 的 坐标的部分。

所以，对于枚举到的点 ，我们需要找到它前面第一个 坐标不大于它的点 ，如果称 的 坐标为 ， 的 坐标为 的话，我们需要考虑下半部分 坐标在 的点。我们希望快速找到这样的 ，因此对于上半部分可以维护一个 坐标单调不减的栈。如果要加入的点 坐标比栈顶小，则弹栈，直到要加入的点 坐标大于等于栈顶的 坐标。那么现在栈顶的 坐标与要加入的点的 坐标之间的区域就是下半部分要考虑的点。

对于下半部分，仍然按从左到右的顺序考虑，如果有 坐标相同的情况，则只考虑 坐标最大的那个，因为所有 坐标比它小的点构成的矩形一定包含 坐标最大的这个。考虑下半部分一个点如果对答案有贡献，当且仅当这个点之后没有 坐标大于等于它的，由于如果这个点可以成为答案并且后面有一个点 坐标大于等于它，那么这个点就会在答案形成的矩形中，不符合定义。由于按顺序考虑，如果下半部分的某个点对答案无贡献，那么在所有情况中这个点对答案都没有贡献。因此顺序考虑下半部分的点，维护 坐标单调减的栈。如果要加入的点 坐标大于等于栈顶，则弹栈，直到要加入的点 坐标小于栈顶的 坐标。枚举完成后，栈中剩余元素就是所有我们需要考虑的可能对答案有贡献的点。

之后，对于上层枚举到 ，前面第一个 坐标不大于它的点为 的情况，我们只需统计下半部分的栈中有多少点的 坐标在 区间内，使用二分法找出 坐标第一个大于 的位置和最后一个小于等于 的位置即可。

综上，选定上半部分的某一个点为右上角的情况对答案的贡献已经处理完毕。选定上半部分的某一个点为左上角的情况与其类似，我们只需要将所有点沿 轴对称，重复上述算法即可，考虑等价性，沿 轴对称的点分布统计上半部分的某一个点为右上角的情况等价于原来点分布统计上半部分的某一个点为左上角的情况。

至此，第 3 步已经处理完毕。

考虑时间复杂度，我们按照 这条水平线分割，但是有可能有许多点的 坐标均为 。当出现这种情况时，我们选择这些 的样本中点进行上下部分分割。由于我们已经考虑了 相同情况的处理，所以这样分割的正确性也可以保证。并且从样本中点分割可以保证分成的两个子问题大小均为 ，保证时间复杂度不会变差。

我们在考虑上半部分时，每个点会被枚举一次，并且由于出栈后的点不会在入栈，因此出入栈最多一次，在考虑下半部分时，同样每个点被枚举一次，出入栈最多一次。所以在处理上半部分的区间和下半部分对答案有贡献的点的时间复杂度为 。对于统计答案，由于 和 相关，我们枚举了每个 ，并在下半部分的栈中进行二分。因此这部分时间复杂度为 。因此可以写出递归式 。使用迭代法求解，可知这个算法的时间复杂度为 。

原题为 JOISC 2014 稻草人，代码可以参考这里。只需要把点按 轴对称就变成了这个题了。

八、输入含有 个顶点的加权二叉树 和正数 ，树 上每条边的权值都非负，树中顶点 的距离 定义为从 到 的各边权值之和。试设计一个分治算法输出满足 的顶点对个数，并分析时间复杂度。

考虑对树进行点分治，定义一棵树的重心为如果以这个点为根，没有任何点的子树大小超过 ，其中 为这棵树的节点个数。

考虑先找到一棵树的重心，将其分为一些子树。那么所有点对之间的路径就可以分为如下两种情况：

  1. 点对之间路径完全在一个子树中；
  2. 两点分别位于两不同子树（或其中一点为重心），易知这条路径一定过重心；

考虑情况 1，为原问题的一个子问题，首先找出其子树的重心，然后递归地调用该算法即可。对于找出一棵树的重心，可以先统计出这棵子树中每个节点以它为根时每棵子树大小，之后根据定义找到重心。我们可以类似前缀和地统计，对于「向上」的子树大小，为整棵树的大小减去以这个节点为根「向下」的所有子树大小之和。因此统计中树上节点全部被统计一次，时间复杂度为 。

考虑情况 2，由于需要统计 且 在不同子树的点对数量，而情况 2 中的路径一定过重心，那么 就等于 ，其中 为重心。那么要统计的值就等于这棵树中所有 的点对数量减去其中 在同一子树的点对数量。

实际上两个问题性质相同，考虑如何统计 的点对数量。可以先统计以 为根的子树中所有节点（包括 ）到 的距离，记为 。由此原问题转化为统计有多少无序数对 ，其中 ，使得 。相当于统计有多少有序数对 ，其中 满足前述不等式。

考虑对 排序，若我们枚举 。由于单调性，在 增大时要使和式小于 ， 不会向右移动。因此使用尺取法，每次 枚举到下一个位置时， 随之向左调整到满足不等式的最右端位置。那么这次调整将为 产生 对满足条件的数对。当 时，由于需要满足有序数对的要求，算法结束。

分析上述统计过程的时间复杂度，首先排序带来了 的复杂度。对于之后的统计，由于 单调向右移动， 不动或始终向左移动，当 时停止。这个过程中序列中每个元素最多访问一次。因此这个统计过程的复杂度是 。综上，整体统计过程复杂度为 。

由于一条路径要么过重心，要么不过重心。在问题分解时情况已经考虑完全，子问题之间没有重复，因此算法正确性易得。

由于重心的子树没有任何点子树大小超过 ，那么最差情况为一条链。会将原问题分解为两个规模为 的子问题。然后我们需要找出每个子树的重心，时间复杂度为 。对于情况 2，已经分析出复杂度为 。综上时间复杂度可以写作递推式 ，使用迭代法计算可知这种分治算法时间复杂度为 。

点分治入门题，可以在坟里看。

九、给定平面上 个点坐标 构成的集合 ，，，试设计一个分治算法，输出 中的三个点，使得以这三个点为定点的三角形周长达到最小，并分析时间复杂度。

考虑使用与求平面最近点对类似的算法。假设目前要处理的点集 中点已经按照 坐标从小到大排好序了。

如果 中有少于三个点，则直接退出。如果 中有三个点，如果这三个点可以构成三角形后返回这个三角形，同时将其按 坐标从小到大排序。

否则，计算 中各点 坐标中位数 ，用垂线 将点集分为大小相等的左右两部分。并递归地在左右寻找周长最小的三角形。

令 为左半部分周长最小三角形的周长， 为右半部分周长最小三角形的周长，记 。合并左右两边时，可以知道合并的情况是左边贡献一个点，右边贡献两个点，或左边贡献两个点，右边贡献一个点。考虑在某边取一个点，假设这个点选在 区间，我们无论第二个点选在哪里，这个三角形的周长均会大于 。由于三角形两边之和大于第三边，这样选择点，总会使得三角形存在一条长度大于 的边，使得周长超过 。因此只需考虑横坐标在 区间内的点即可。

再基于同样考虑，选定了一个点 ，假设它的纵坐标为 ，我们只需考虑纵坐标在 的点作为第二和第三个点。此时左右部分 坐标均按从小到大排序，按照归并排序的思路将左右两部分点按 坐标二路归并。对于横坐标在考虑范围内的点，按纵坐标从小到大的顺序枚举选定点 。如果确定了一个点 就确定了一个考虑范围，由于按纵坐标从小到大的顺序枚举点 ，所以这个考虑区间只会向上移动，使用双指针框定考虑范围后暴力枚举第二和第三个点即可，判断其是否可以构成三角形后更新答案。

对于这部分复杂度，和最近点对同样采用画格法考虑，由于对于每一个 ，需要考虑的范围内点数为常数，那么其平方也为一常数。所以合并左右两部分求出这部分的答案的复杂度为 。

综上，我们每步将问题分解成了两个规模为 的子问题，同时对 坐标归并排序，并更新答案的时间复杂度为 。因此可以写出递归式 ，根据 Master 定理可知此算法时间复杂度为 。

原题来自 BJWC 2011 最小三角形，顺便重写了一下严格 的最近平面点对，在这里。注意做比较的时候距离是有平方的，水平和竖直方向上的距离求完坐标差之后要平方。

十、设 是由不同实数组成的数组，如果 且 ，则称实数对 是该实数组的一个反序。如，若 ，则该数组存在 个反序 ， 和 。反序的个数可以用来衡量一个数组的无序程度。试设计一个时间复杂度严格低阶于 的分治算法，计算给定数组的反序个数，并分析时间复杂度。

考虑归并排序的同时统计逆序对数量。首先将序列从中间分为两部分。即，对于序列 ，考虑分为 和 两部分。其中 。

递归统计两个部分内部的逆序对数量并归并排序后，将左右两部分有序序列归并并统计左边对右边逆序对的影响。考虑二路归并时左边出现了一个大于右边的数，这就证明出现了逆序对。每次后段首元素被作为当前最小值取出时，前段所有剩余元素都会与这个元素形成一个逆序对，因此前段剩余元素个数即是后端首元素对逆序对的贡献。因此，分割后归并的同时统计逆序对数量即可。

对于分割部分，我们分割成了两个互不相交的子问题，二路归并中，所有元素均被访问一次，统计逆序对仅需要计算前段数组长度与现在前段的指针位置的差值，时间复杂度为 ，因此二路归并的复杂度为 。

综上，可以写出递归式 。使用主定理可以计算复杂度为 。此复杂度严格低阶于 。

第二次作业

动态规划

一、设你要爬 阶楼梯。 每一次，你可以爬 个或者 个台阶。计算总共有多少种方法可以爬完？如：，则有三种，分别是 。

1. 证明该问题的优化子结构，说明子问题的重叠性。
2. 给出状态转移方程和初始条件，并写出伪代码。
3. 分析算法复杂度。

1. 本问题为一计数问题而非优化问题。令现在我们位于第 级台阶，若要一步登上第 级台阶，那么要么是从第 级台阶爬一步登上来的，要么是从第 级台阶爬两步登上来的。根据分类加法计数原理，登上第 级台阶的方案数取决于登上第 级台阶的方案数与登上第 级台阶的方案数。可以令 表示登上第 级台阶的方案数。子问题即为求出每个登上第 级台阶的方案数。

2. 由 1 可知，状态转移方程为： 初始条件为 。伪代码如下

1
2
3
4
5
CountStep(n)
f[1] = 1, f[2] = 2
for i = 3 to n do
    f[i] = f[i - 1] + f[i - 2]
return f[n]

3. 由状态转移方程，共有 次转移，每次转移的复杂度为 ，所以整体时间复杂度为 ，空间复杂度也为 。

实际上 为 Fibonacci 数列，有 的矩阵快速幂求法。

二、考虑三个字符串 的最长公共子序列 。

1. 寻找反例 使得 不等于 。
2. 设计动态规划算法计算 的最长公共子序列。 写出伪代码， 并分析算法的时间复杂度。

1. 考虑 ，那么 ，但是 或 ，因此 。

2. 类似 LCS 在两个串情况下的求法，优化子结构如下：设 ， 是 的最长公共子序列，有：

  1. 如果 ，则 ，；
  2. 如果不满足 ，且 ，则 ；
  3. 如果不满足 ，且 ，则 ；
  4. 如果不满足 ，且 ，则 ；

对于 (1)，设 ，则可加 到 ，得到一个长为 的最长公共子序列，与定义矛盾，所以 。设存在 的非最长公共子序列 ，使得 ，则由于 ，，与定义矛盾，所以 (1) 成立。

对于 (2)，由于 ，设存在 的最长公共子序列 的长度大于 ，则 也是 的最长公共子序列长度，与定义矛盾。所以 (2) 成立。

对于 (3)，(4)，证明同 (2)。

因此令 为 的最长公共子序列长度，转移方程为

伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
LCS-length(X, Y, Z)
n = length(X), m = length(Y), l = length(Z)
for i = 0 to n do
    for j = 0 to m do
        for k = 0 to l do
            f[i, j, k] = 0
for i = 1 to n do
    for j = 1 to m do
        for k = 1 to l do
            if X[i] = Y[j] and Y[j] = Z[k] then
                f[i, j, k] = f[i - 1, j - 1, k - 1] + 1
                B[i, j, k] = 1
            else
                if f[i - 1, j, k] is max of {f[i - 1, j, k], f[i, j - 1, k], f[i, j, k - 1]} then
                    f[i, j, k] = f[i - 1, j, k]
                    B[i, j, k] = 2
                else if f[i, j - 1, k] is max of {f[i - 1, j, k], f[i, j - 1, k], f[i, j, k - 1]} then
                    f[i, j, k] = f[i, j - 1, k]
                    B[i, j, k] = 3
                else
                    f[i, j, k] = f[i, j, k - 1]
                    B[i, j, k] = 4
return f and B
Print-LCS(B, X, i, j, k)
if i = 0 or j = 0 or k = 0 then
    return
if B[i, j, k] = 1 then
    Print-LCS(B, X, i - 1, j - 1, k - 1)
    Print(X[i])
else if B[i, j, k] = 2 then
    Print-LCS(B, X, i - 1, j, k)
else if B[i, j, k] = 3 then
    Print-LCS(B, X, i, j - 1, k)
else
    Print-LCS(B, X, i, j, k - 1)
return

对于求最长公共子序列长度，可知有 （）次转移，每次转移的复杂度为 ，所以整体的时间复杂度为 （），空间复杂度为 （）。

对于输出最长公共子序列，时间复杂度为 （），空间复杂度为 （）。

三、给定一个 的网格，网格中全是非负的整数。找出一条从该网格左上角到右下角的路径，使得路径上数字总和最小。每次只能向下或者向右移动一步。

设 表示从左上角到达 的路径上的最小数字和。为了到达 ，可以从 向下移动一步，或者从 向右移动一步走到，转移方程可以写作

伪代码为

1
2
3
4
5
6
7
8
9
MinSum(n, m)
for i = 1 to n do
    f[i, 1] = f[i - 1, 1] + a[i, 1]
for i = 1 to m do
    f[1, i] = f[1, i - 1] + a[1, i]
for i = 2 to n do
    for j = 2 to m do
        f[i, j] = min(f[i, j - 1], f[i - 1, j]) + a[i, j]
return f[n, m]

可知时间复杂度为 ，空间复杂度为 。

四、给定一个整数序列 。相邻两个整数可以合并，合并两个整数的代价是这两个整数之和。通过不断合并最终可以将整个序列合并成一个整数，整个过程的总代价是每次合并操作代价之和。试设计一个动态规划算法给出序列 的一个合并方案使得该方案的总代价最大。你的答案应包括：

1. 用简明的语言表述这个问题的优化子结构。
2. 根据优化子结构写出代价方程。
3. 根据代价方程写出动态规划算法（伪代码）并分析算法的时间复杂性。

1. 若计算 的最大合并代价，假设从 处断开，则合并出 的子问题的解必为其优化解，合并出 的子问题的解必为其优化解。

2. 令 为合并 的最大合并代价，则转移方程为

其中 。

3. 伪代码如下

1
2
3
4
5
6
7
8
9
10
11
Merge(n)
for i = 1 to n do
    f[i, i] = 0
    s[i] = s[i - 1] + a[i]
for l = 2 to n do
    for i = 1 to n - l + 1 do
    j = i + l - 1
    f[i, j] = 0
    for k = i to j - 1 do
        f[i, j] = max{f[i, j], f[i, k] + f[k + 1, j] + s[j] - s[i - 1]}
return f[1, n]

根据伪代码，可知此算法时间复杂度为 。

五、输入凸 边形 其中顶点按凸多边形边界的逆时针序给出，多边形中不相邻顶点间的连线称为弦。试设计一个动态规划算法，将凸边形 剖分成一些无公共区域的三角形，使得所有三角形的周长之和最小。写出伪代码，并分析算法的时间复杂度。

设 是 个顶点的多边形，如果 是 的包含三角形 的优化三角剖分，即

则 是 的最优三角剖分，则 是 的最优三角剖分。

设 为 这个优化三角剖分的代价，则

其中 是三角形 的周长。

伪代码如下

1
2
3
4
5
6
7
8
9
10
MinC(n)
for i = 0 to n do
    f[i, i] = 0
for l = 2 to n do
    for i = 2 to n - l + 1 do
    j = i + l - 1
    f[i, j] = infty
    for k = i to j - 1 do
        f[i, j] = min{f[i, j], f[i, k] + f[k + 1, j] + C(a[i - 1], a[j], a[k])}
return f[1, n]

由伪代码可知，时间复杂度为 。

贪心算法

一、一棵树，结点个数为 ，根结点为 。每个结点都有一个权值 ，开始时间为 ，每染色一个结点需要耗时 ，每个结点的染色代价为 （ 为当前的时间），每个结点只有在父结点已经被染色的条件下才能被染色。求对整棵树完成染色需要花费的最小代价 。

1. 给出贪心策峈；
2. 证明贪心选择性和优化子结构；
3. 写出伪代码并分析算法复杂度。

1. 考虑等价问题：求一个点的排列 ，满足对任意非根节点，父节点排在自己前面，排列的代价为 ，求最小代价。

由排序不等式，考虑让权值大的点排在前面，而在选这个权值最大的点前要先选父节点。考虑一个合法的排列 ，如果 不是 的父亲，且 的权值比 小，则由排序不等式，交换这两项结果更优。不断重复上述过程，可以发现权值最大的点一定紧跟在它的父节点后面。由此，考虑有两个集合 和 先后被染色， 和 互不影响，这两个集合实际上为不相交的两棵子树。考虑先合并 再合并 为最优，则满足

化简后有

可以解释为：已经预合并了两段点 和 ， 中先出现 再出现 当且仅当上式成立。

2. 贪心选择性：第一次一定选择权值最大的点与父亲合并。如果不是，设权值最大的节点为 ，如果其为根节点，那么它一定在第一次合并，否则设其父亲为 ，则此时的代价为

交换 和 ，不妨假设这次操作不影响 染色的合法性，则代价为

由于 且 ，则下式更小。因此第一次选择一定选择权值最大的点与父亲合并。

优化子结构：考虑已预合并的两端要合并起来，方法同 (1) 中说明。

3. 伪代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
Color(n)
S = {}, ans = 0
for i = 1 to n do
    Insert(S, c[i])
while S is not empty do
    x = Extract-max(S)
    f = Tree-top(x)
    Union(x, f)
    Delete(S, f)
    ans += c[x] * siz[f]
    c[f] += c[x], siz[f] += siz[x]
    Insert(S, c[f] / siz[f])
return ans

首先将这些点插入平衡树中，时间复杂度为 。然后不断取出预合并段权值和与大小比值最大的段，我们把一个预合并段的信息存在树上这个预合并段中深度最浅的节点，用并查集维护。我们把这个预合并段合并在最高点的父节点所在的预合并段上，假设这个预合并段的权值和为 ，则接在父节点后面会产生 的贡献，将其计入答案，然后将下面段的信息合并到父节点所在的段上。

对于这棵平衡树，每次操作都减少一个元素，合并两预合并段的时间复杂度需要先进行平衡树上查询，再进行并查集的查询和合并，然后进行一次平衡树的权值修改（用一次删除和一次插入表示），时间复杂度为 ，因此整体复杂度为 。

实际上为 POJ 2054，代码在这里

二、给定两个大小为 的正整数集合 和 。对于 到 的一个一一映射 ，不妨设 ，则 的代价为 。试设计一个贪心算法，找出从 到 的代价最大的一一映射。

每次选择两集合中最大的 ，使 ，这样得到的权值最大。

伪代码如下

1
2
3
4
5
6
MaxF(A, B)
n = Size(A)
sort(A), sort(B)
for i = 1 to n do
    f[a[i]] = b[i]
return f

首先我们分别对 和 排序，时间复杂度为 ，然后遍历 和 中所有元素，时间复杂度为 ，因此整体复杂度为 。

正确性证明如下。

1. 贪心选择性：对排序后（从大到小）的 中元素分别表示为 和 ，只需证优化解中存在 。

假设优化解中不存在 ，而是 ，则此时，映射的代价为

而交换这两个映射，代价为

考虑 ，令 ，则 。由于 ，则有 ，而 都是正整数，所以 在 时恒成立，因此 在 时恒成立， 单调不减。而 ，所以 ，即 ，因此 。

由以上，做一次交换不会使代价变劣，原假设不成立。因此优化解中存在 。

2. 优化子结构：只需证 是问题 的优化解。若存在 是问题 的优化解，则 ，而加上 的代价后，有 ，这样又构造出了一个比原问题优化解更优的解，不成立。所以原命题得证。

综上，上述贪心算法的正确性得证。

三、给定平面点集 和 。 支配 当且仅当 且 。试设计一个贪心算法输出集合 且 支配 ，使得该集合中点对最多。

首先由于要输出集合，因此最差情况下不可避免遍历 中所有点，因此暴力枚举判断的复杂度即为复杂度上限。

至于贪心算法，本题可转化为：平面上目前已有点集 ，而 不在平面上。枚举 中每个点 ，询问 的左下方的所有点 。这个过程是一个计数过程，不存在优化问题，因此无需贪心算法。

怎么改题意之后想都是一个计数问题，比如找左下方没有点的最大子集什么的，那直接二维偏序就好了。总感觉我和出题人总有一个题意挂了。

四、一个 DNA 序列 是字符集 上的串，其上有大量信息冗余。设 是 的子串， 及其冗余形式在 内在出现的起、止位置构成了一系列等长区间 。试设计一个贪心算法找出 的一个最大子集，要求子集中的区间两两不相交。

1. 给出贪心策略；
2. 证明贪心选择性和优化子结构；
3. 写出伪代码并分析算法复杂度。

1. 按右端点从小到大排序后枚举每个区间，先将第一个区间加入几何，然后只要当前区间左端点在集合中最后一个区间的右端点右边，就选择这个区间加入集合。

2. 贪心选择性：设 是一个优化解，按结束位置排序这些区间，设第一个区间为 ，第二个区间为 。如果 ，则命题成立，若 ，令 ，由于 中的区间互不相交，且 ，则 中的区间也互不相交，则 ，所以 也是一个优化解，且包含区间 。

优化子结构：设 是一个包含 的优化解。则 是问题 的优化解。显然 中区间互不相交，只需证 是最大的。若不然，则存在一个 的问题优化解 ，且 ，令 ，对于任意 ，都有 ，所以插入后 中区间也是互不相交的，则 是 的一个解。由于 ，则 ，因此与 为最大矛盾，因此此问题具有优化子结构。

3. 伪代码

1
2
3
4
5
6
7
8
9
IntervalSelect(P, Q)
sort(P, Q)
S = {1}
j = 1
for i = 2 to n do
    if P[i] > Q[j] then
        Append(S, i)
        j = i
return S

首先对线段按照右端点从小到大排序，时间复杂度为 ，之后枚举每条线段，时间复杂度为 。因此整体时间复杂度为 。

五、某工厂收到 个订单 ，其中 和 均是正整数，订单 希望在时间 之前获得 件产品。工厂的生产能力为每个时间单位生产 件产品。工厂希望拒绝最少数量的订单，并恰当地排序剩下的订单使得剩下的订单均能够被满足。试设计一个贪心算法求解上述问题。

首先排除一定不能完成的订单，即 的订单。排除后按 从小到大排序，之后枚举每个订单，如果这个订单可以完成，则加入可满足的订单列表，否则拒绝它。

贪心选择性：考虑 是一个优化解，设第一个订单为 ，第二个订单为 。若 则命题成立，若 ，令 ，由于 ，不妨设 ，则 ，则将 换为 ，有 ，因此这种交换合法，且 ，则 也是一个优化解，且包含 。

优化子结构：设 是包含 的优化解，则 为剩余问题的优化解。若不然，则存在优化解 ，满足 ，令 ，由于剩余问题中保持了 的产能，所以插入后 中所有订单都可以生产，则 是一个解。由于 ，则 ，因此与 为最大矛盾，因此此问题具有优化子结构。

伪代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
MinReject(n, a, b)
sort(a, b)
sum_a = IntervalTree(n)
min_b_sa = IntervalTree(n)
accept = []
for i = 1 to n do
    if b[i] > a[i]
        continue
    if Sum(sum_a, 1, b[i]) + a[i] > b[i] then
        continue
    if Min(min_b_sa, b[i], INF) < a[i] then
        continue
    sum_a[b[i]] += a[i]
    min_b_sa[b[i] .. INF] -= a[i]
    Insert(accept, (a[i], b[i]))
return accept

由伪代码，排序的复杂度为 。维护两棵线段树，第一棵维护现在可以完成的所有任务的 的和，第二棵维护每个任务的截止时间减去它之前所有可以完成的任务的 的和的最小值。

之后遍历每个任务，首先检查目前的任务是否满足可以在截止时间的时候完成，通过第一棵线段树查一下前缀和即可，然后检查插入这个任务后是否会使之前插入的任务不能完成，即第二棵线段树以 为后缀的差的最小值应大于等于 。如果存在一个不满足，则无法满足这个任务的要求，否则加入生产计划，并相对地进行线段树上修改。

每次线段树上查询和修改的时间复杂度均为 ，因此整体时间复杂度为 。

实际上为 「JSOI2007」建筑抢修，代码在这里。当然 std 应该是按 从小到大排序，统计 ，如果目前计划生产的 总和大于 ，就删掉最大的 。这样满足正确性，并且空出了最大余量，满足最优性，但是我不会形式化地写证明……

六、有 个石子，每个石子的重量为 ，现将其聚集成一堆，要求每次只能操作两堆进行合并，每次操作的代价是操作石子重量的和，那么请设计一个方案使聚集的总代价 最小。

1. 给出贪心策略；
2. 证明贪心选择性和优化子结构；
3. 写出伪代码并分析算法复杂度。

1. 每次选择重量最小的两堆石子 合并为一堆。

2. 贪心选择性：考虑合并过程中形成的二叉树，若第一次合并未选择重量最小的两个石子，而将其中一个换为 的石子，那么这次交换将带来 的贡献。由于先合并会带来更多的合并轮次，因此 ，所以贡献为 ，因此交换可能带来更大的代价，所以按重量最小的两堆合并得到的代价是最小的。

最优子结构：设 是第一步合并重量最小的两堆石子的优化解，则 是剩余问题的优化解。若不然，则将这个优化解并上第一步将获得更小的代价，与假设矛盾。

3. 伪代码如下

1
2
3
4
5
6
7
8
MergeStone(W)
n = |W|, Q <- W 且 Q 是小顶堆, ans = 0
for i = 1 to n - 1 do
    x = Extract-min(Q)
    y = Extract-min(Q)
    ans += x + y
    Insert(Q, x + y)
return ans

首先构建小顶堆的复杂度为 ，然后每次循环取得最小值和插入堆的时间复杂度为 ，因此整体时间复杂度为 。

第三次作业

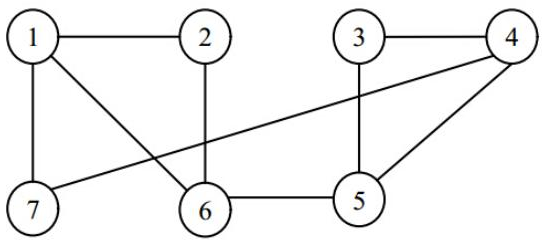
一、在下图中考虑哈密顿环问题。将问题的解空间表示成树，并分别利用深度优先搜索和广度优先搜索判定该图是否存在哈密顿环。

首先要画搜索树，但是搜索树太大了，自己画吧。

使用深度优先搜索，伪代码如下：

1
2
3
4
5
6
7
DFS(G)
1. 构造由 {1} 组成的单元素栈 S
2. If Top(S) 的长度为 8 Then 输出 Top(S)，停止
3. Else T = Top(S), Pop(S)
4, 将每个与 T 的最后一个元素相连，且不在 T 中的元素（除 1 以外）加入 T，压入 S
5. Goto 2
6. If S 空 Then 无解

使用广度有限搜索伪代码如下：

1
2
3
4
5
6
7
BFS(G)
1. 构造由 {1} 组成的单元素队列 Q
2. If Q 的首元素长度为 8 Then 输出首元素，停止
3. Else T = Q 的首元素, 弹出 T
4. 将每个与 T 的最后一个元素相连，且不在 T 中的元素（除 1 以外）加入 T，加入 Q
5. Goto 2
6. If Q 空 Then 无解

二、考虑 8-魔方问题。分别用爬山法，最佳优先方法判定上图所示的初始格局能够通过一系列操作转换成目标格局，将搜索过程的主要步骤书写清楚。

话说这玩意不叫八数码吗……

使用爬山法，令启发式测度函数 ，其中 是节点 中处于错误位置的方块数，扩展结点时，按 从大到小的顺序压栈，让 小的节点先扩展。伪代码如下：

1
2
3
4
5
1. 构造由初始局面组成的单元素栈 S
2. If Top(S) 是目标局面 Then 停止
3. Pop(S)
4. 对于 Top(S) 的所有可能移动，按新局面 f(n) 从大到小的顺序压入 S
5. If S 空 Then 无解 Else goto 2

使用最佳优先方法，根据评价函数 ，在目前产生的所有节点中选择具有最小评价函数值的节点进行扩展。伪代码如下：

1
2
3
4
1. 使用评价函数构造小根堆 H，将初始局面插入 H 中
2. If H 的根 r 是目标局面 Then 停止
3. 从 H 中删除 r，将 r 移动后所有可能的局面插入 H
4. If H 空 Then 无解 Else goto 2

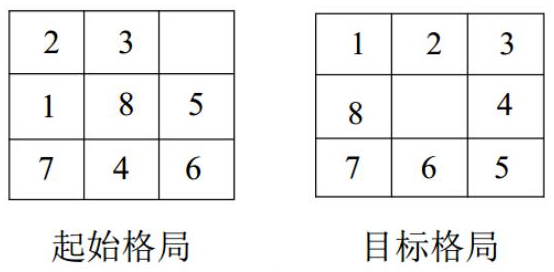
三、精确描述求解 8-魔方问题的 A* 算法，在习题 2 给出了起始格局和目标格局上给出 算法操作的主要步骤。

1. 设计 ，， 和 ，以满足 A* 算法的要求；
2. 以第 2 题给出的起始和目标格局，写出 A* 算法运行的主要步骤，并标明每一步 ， 的值。

1. 令 为从初始局面变为局面 所经历的步数， 为局面 与目标局面之间，相同数码在两个棋盘中的曼哈顿距离之和， 为从局面 到目标局面经历的步数，。

2. 过程如下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
    2 3 0
    1 8 5
    7 4 6

1.  2 0 3             2 3 5
    1 8 5 g(n) = 1    1 8 0 g(n) = 1
    7 4 6 h(n) = 7    7 4 6 h(n) = 10

2.  0 2 3             2 8 3
    1 8 5 g(n) = 2    1 0 5 g(n) = 2
    7 4 6 h(n) = 6    7 4 6 h(n) = 8

3.  1 2 3
    0 8 5 g(n) = 3
    7 4 6 h(n) = 5

4.  1 2 3             1 2 3
    8 0 5 g(n) = 4    7 8 5 g(n) = 4
    7 4 6 h(n) = 4    0 4 6 h(n) = 6

5.  1 2 3             1 2 3
    8 4 5 g(n) = 5    8 5 0 g(n) = 5
    7 0 6 h(n) = 3    7 4 6 h(n) = 5

6.  1 2 3             1 2 3
    8 4 5 g(n) = 6    8 4 5 g(n) = 6
    7 6 0 h(n) = 2    0 7 6 h(n) = 4

7.  1 2 3
    8 4 0 g(n) = 7
    7 6 5 h(n) = 1

8.  1 2 3
    8 0 4 g(n) = 8
    7 6 5 h(n) = 0

四、分别使用深度优先法和分支限界法求解子集和问题的如下实例。

输入：集合 和整数 。
输出： 使得 中元素之和等于 。

使用深度优先搜索伪代码如下：

1
2
3
4
5
1. 构造由空集组成的单元素栈 S
2. If Top(S) 的集合元素和为 K Then 停止
3. 令 C = Top(S), Pop(S)
4. 对于每个不在 C 中的元素 x，C <- C ∪ {x}，将 C 压入 S
5. If S 空 Then 无解 Else goto 2

使用分支界限法可以缩小解空间的范围，伪代码如下：

1
2
3
4
5
6
1. 构造由空集组成的单元素栈 S
2. If Top(S) 的集合元素和为 K Then 停止
3. 令 C = Top(S), Pop(S)
4. 对于每个不在 C 中的元素 x，如果加入 C 后集合元素和仍
   小于等于 K，则 C <- C ∪ {x}，将 C 压入 S
5. If S 空 Then 无解 Else goto 2

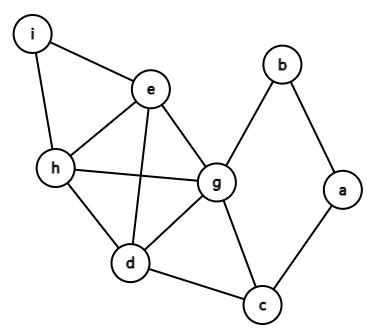
五、利用搜索求下图的最大完全子图（团），要求写出计算过程。

抄一下 Bron–Kerbosch Algorithm。

第四次作业

随机算法

一、一个木桶里有 个白球，每分钟从桶里随机取一个球涂成红色（无论白球或红球都涂红）再放回，问将桶中的球全部涂红的期望时间是多少？

令 表示木桶里有 个红球时，还需要抽取直到可以将所有球都染成红色的期望时间。对于当前状态， 的计算可以分为两部分：此时抽到红球和此时抽到白球。此时抽到红球的概率为 ，抽到白球的概率为 ，所以可知

化简可得

由已知，，则根据归纳法可知

二、传送带上有若干产品，一个质量检测员在传送带某一检测点工作，如果他今天要检测 个产品：

1. 请帮他设计一个检测算法，使得整条传送带上的所有产品被选中的概率相同。
2. 证明该算法使得所有产品被选中的概率相同。

1. 首先取走传送带上前 个产品，放在待检区。对于后续产品 ，生成一个 到 的随机数 ，如果 ，则将待检区中第 个产品替换为产品 ，否则忽略产品 。

等到所有产品都通过后，待检区内的产品就是要检测的产品。

2. 要证：对于传送带上前 个产品，其被抽取的概率均为 。

使用归纳法。当 时，前 个产品均被直接抽取，概率为 。

当第 个产品到来时，这个产品被抽取的概率为 。假设前 个产品任意一个被抽取的概率均为 ，待检区的 个产品中，仍被保留的概率为 ，因此新产品通过后，前 个产品被抽取的概率为 ，符合假设。因此根据数学归纳法，假设成立，上述算法使得所有产品被选中的概率相同。

Reservoir sampling - Wikipedia

近似算法

一、试着修改集合覆盖算法求解加权集合覆盖问题，并分析它的近似比。

可以参考 Encyclopedia of Algorithms 和 UW CSE 525，写得都挺好的，翻译一下就好了。

二、考虑下述场景。给定一个城市集合以及城市之间的距离，从中需要选出 个城市来设置仓库，使得各个城市距离它最近的仓库的距离中的最大者达到最小。这是经典的 K-center 问题，它的形式化定义如下：

输入：平面上的点集 ，欧式距离 ，以及参数 。
输出：定义 的代价是 。要求找到 ，使得 最小。

下面是一个求解 K-center 问题的基于贪心策略的近似算法，请证明它的近似比是 。

可以参考 Metric k-center - Wikipedia 和 Geometric Approximation Algorithms Chap. 4.2。

书里的反证法很巧妙。

在线算法

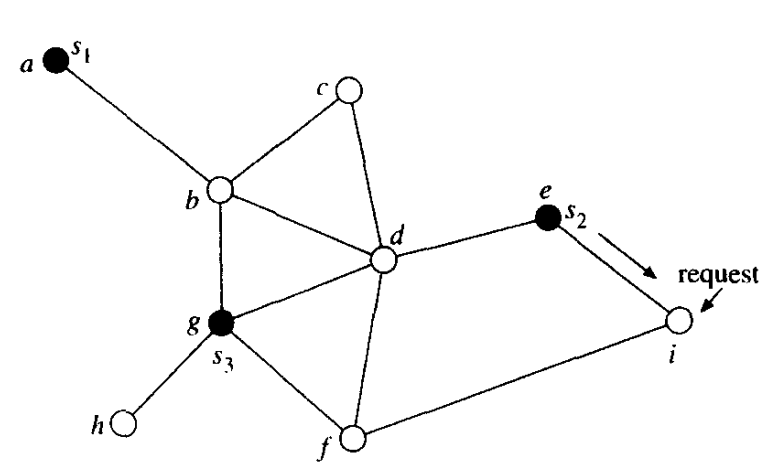
一、已知有 个顶点的图，每条边分配一个正的边长。令在 个顶点分配 名服务员去完成顶点处的请求。对一个请求的服务代价是满足该请求服务员移动的总距离。参见如图所示，有三名服务员 ，分别位于 、 和 ，如果在顶点 有一个请求，由于 靠近 ，那么可能的一种移动方法是把位于顶点 处的 移动到顶点 处，代价为 到 的边长。现在对服务员的请求序列是在线不断提供的，现需要获得全部请求序列最小服务代价。请设计一个在线算法计算最小服务代价并分析竞争比。

是一个 k-server problem，题面就是 Introduction to the Design and Analysis of Algorithms 书里 12.2 节的例子，书在 Z-lib 能下到，注意作者是 R. C. T. Lee，并且书也挺老了，别下错了。但是看证明过程还是看 On-line Computation and Competitive Analysis 10.4 节的，写得很明白。

原论文中要求是完全图，但是一般图也是符合三角不等式的，考虑在最短路树上走就可以了。其实也可以直接看 An Optimal On-Line Algorithm for K Servers on Trees 这篇论文。

期末考试

考试考得贼小丑，虽然考试大部分还是作业里的，但是考前没看，哈哈。

先上来考的求时间复杂度，反正递推一下就行，一个主定理也不难。

然后是一个求哈密顿圈的分支界限搜索，要画搜索树，反正也就那么画。

然后是一个贪心，给了 个区间，保证可以覆盖 ，问最少要多少区间才能覆盖 。是 LOJ #10002，在考场上纠结怎么排序，笑死。

然后是一个 DP，求最大子段和，随便搞搞就行了。

随机算法考的蓄水池抽样，但是要抽连续 个，我不会。

近似算法考的是一般图最小权覆盖的近似算法，就在 PPT 上但是我没看，近似比 我写了个 ……